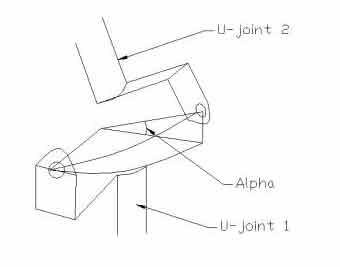
Calculation of U-Joints

Spreadsheet for how the graphs were generated on CV joint error

Several methods can be used to derive the phase error on a single U-joint. Below shows one method. Phase error on a CV joint is calculated the same way as a single u-joint, but using two of them. Use simple geometry to determine the angle of each of the u-joint in a CV joint. See Klein Gelenkwellen - CV-joint on description of why CV joint have phase error along with some equations.

Derive phase error of a single U-Joint

U-joint 1 (one half of the U-joint) is rotating on the vertical axis. U-Joint 2 (the other half of the U-joint) is rotating on an inclined axis. The two axis intercept at the center of the joint. The operating angle is Alpha. The path of the outer edge of the two u-joint halves will trace two circles. Only quarter of the circle is shown. The radius of one circle will represent the cross arm of one u-joint halve, and the radius of the other circle will represent the cross arm of the the other u-joint halve. The two radius will always have to be right angle to each other since the arms of the u-joint cross is always at right angle.

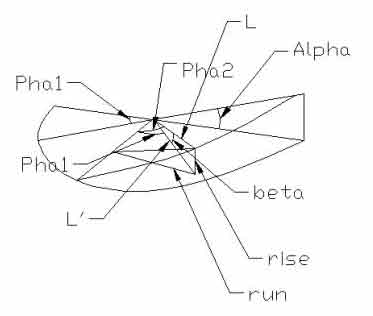
tan (alpha)= slope = rise/run

1) L sin (beta) = rise

2)L cos (beta) = L'

3) L' sin (pha1) = run

Combine the equation 1-4:

4) tan (alpha) = (L sin (beta)) / (L cos (beta) * sin (pha1))

Solve for beta:

5) beta = atan (tan(alpha)*sin(pha1))

Determine hypotenuse, h:

6) h sin (alpha) = rise

Combine equation 2 & 5 and solve for h:

7) h = (Lsin( atan( tan(alpha)*sin(pha1))) / sin (alpha)

Solve for pha2:

8) L sin(pha2) = h

Combine equation 7:

Pha2 = asin [ sin { atan (tan(alpha)*sin(pha1)) } / sin(alpha) ]

To see the phase error, just subtract Pha2 from Pha1. This equation is only valid for up to 90 degrees because of the sin / cos functions. If you change the alpha to negative, you will find that Pha2 does not change. This proves that a u-joint phase cancellation can be made by rotating the axel either direction.